The gravitational force is much weaker than the electromagnetic force. Most objects made out of normal matter have both positive and negative charge, so much of the effect of the electromagnet force is not noticeable on a large scale. The charges cancel out. Massive particles all attract each other. For a very massive body like Earth, the gravitational force dominates the electromagnetic force overall.

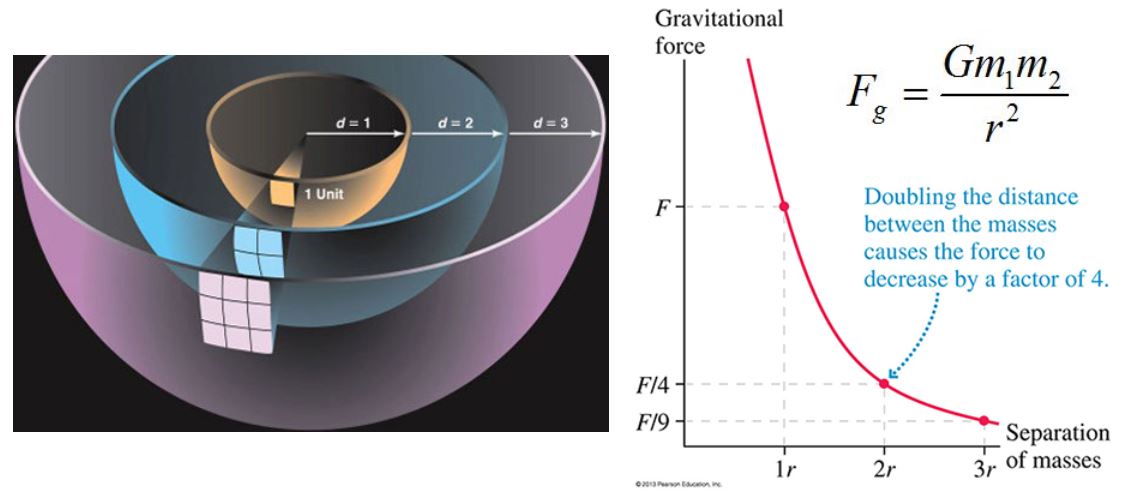
The gravitational force is an inverse square function. As you double the distance between massive particles, the force between them decreases by a factor of four.

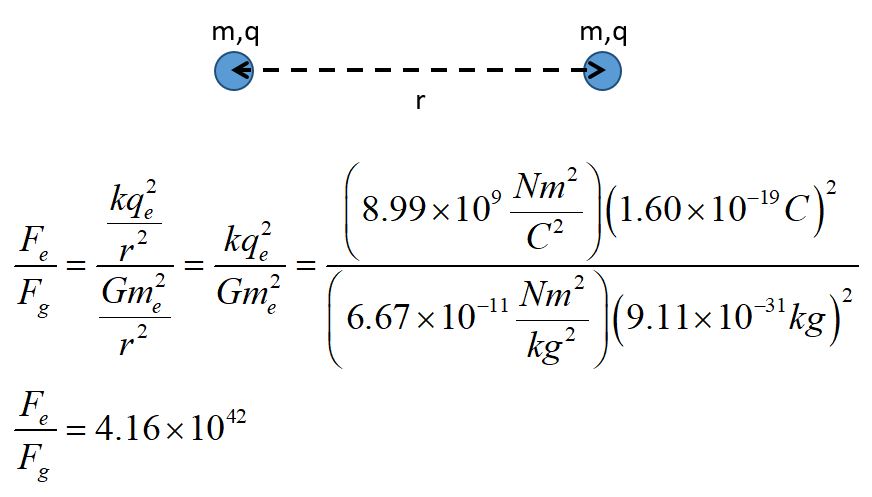
The electromagnetic force is also an inverse square function the comparison of the electromagnetic force and the gravitational force between two electrons reveals the tremendous difference between the strengths of these forces.

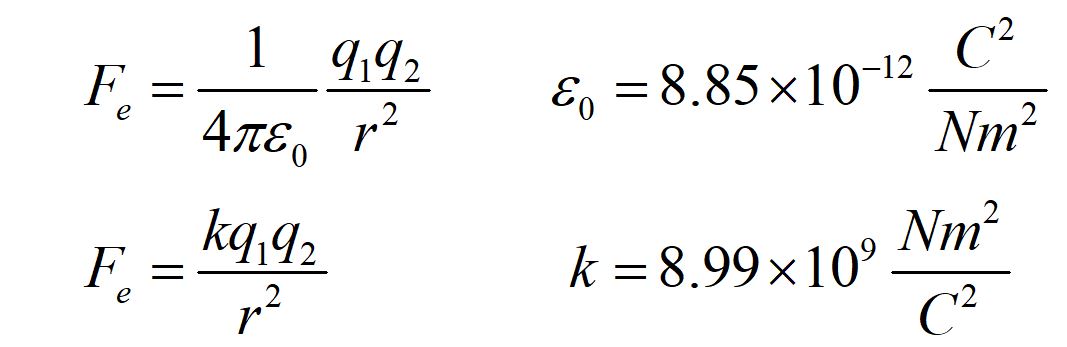
The force between two charges is described by Coulomb's law. Notice that this is a scalar equation as written above. This form just gives the magnitude of the force. The direction of the force must be determined by the signs of the charges. We typically use the variable "q" for the charge. Notice that the charge of an electron in the equation above is given in units of coulombs.

1. Assume these five charges are equally spaced along a straight line. The red charges are positive and the blue charge is negative. Which direction will the charge in the middle accelerate?

   A. right

   B. left

   C. it will not accelerate

2. Six electrons are equally spaced along a straight line. In which direction will the electron fourth from the left accelerate?

   A. right

   B. left

   C. it will not accelerate

3. Four charges lie in a plane, at the corners of a square as shown. In which direction will the positive (red) charge accelerate?

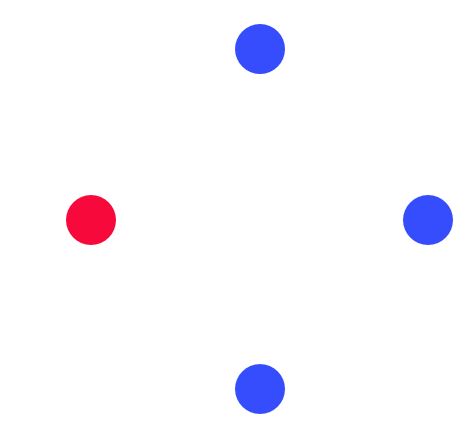
   A. right

   B. left

   C. up

   D. down

   E. none of the above

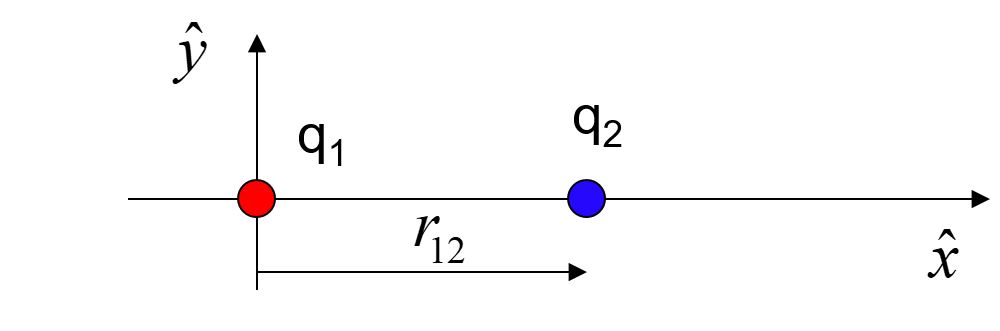
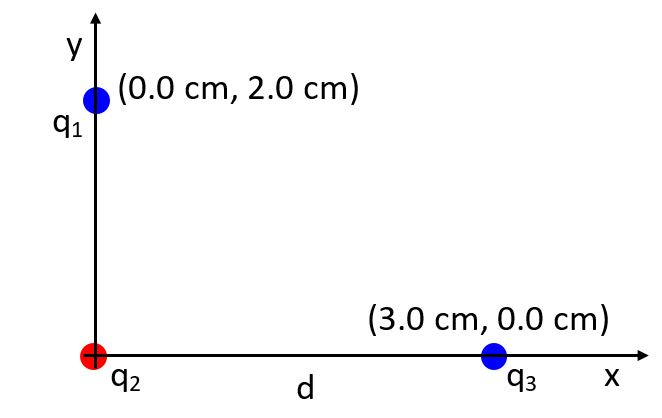
4. Suppose q₁ = -3.0 nC, q₂ = 2.0 nC and q₃ = -4.0 nC. Find the magnitude and direction of the total force on q₂.

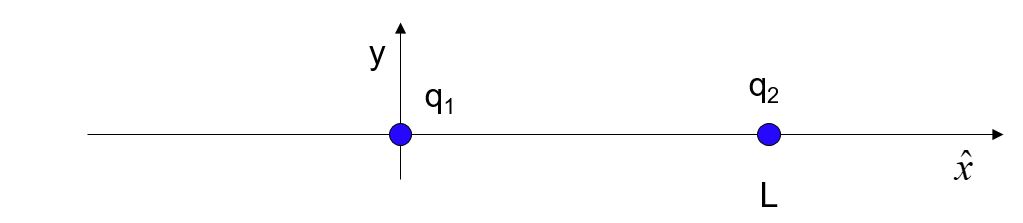
5. Consider the charges as shown, with q₂ = 3q₁. Where could you place a third charge, so that it would not accelerate?

   A. between the charges

   B. left of q₁

   C. right of q₂

6. What would be the sign of the third charge, to make the system in static equilibrium (no charges accelerate)?

   A. positive

   B. negative

   C. either sign would work

7. Consider the charges as shown, with q₂ = -3q₁. Where could you place a third charge, such that the system would be in static equilibrium?

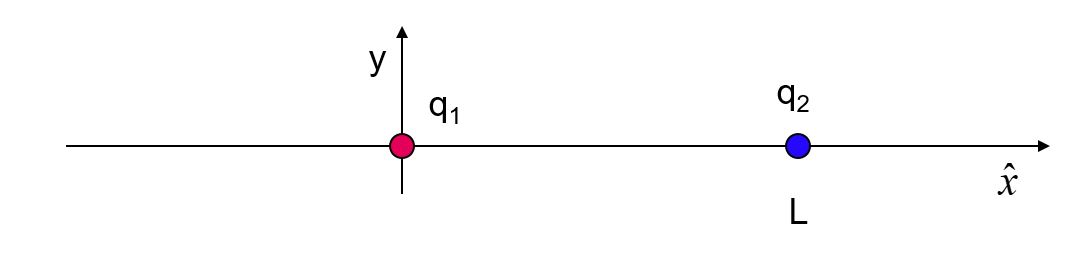
   A. between the charges

   B. left of q₁

   C. right of q₂

8. What would be the sign of the third charge?

   A. positive

   B. negative

   C. either sign would work

9. Consider two charges as shown, 2.00 cm apart. Assume q₁ = 3.00 nC and q₂ = -1.00 nC. Find the magnitude, sign and position of a third charge, q₃, that would make the system in static equilibrium.