Circular motion
- Angular position, velocity and acceleration
- Relationship to translational motion
-
Nonuniform circular motion
- Nonzero angular acceleration
-
Uniform circular motion
- constant speed
-
Derive angular acceleration
- Magnitude and direction
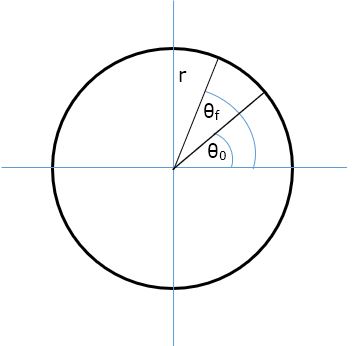
Theta is defined as an angle in a circle of radius r. We have defined the counterclockwise direction to be positive.
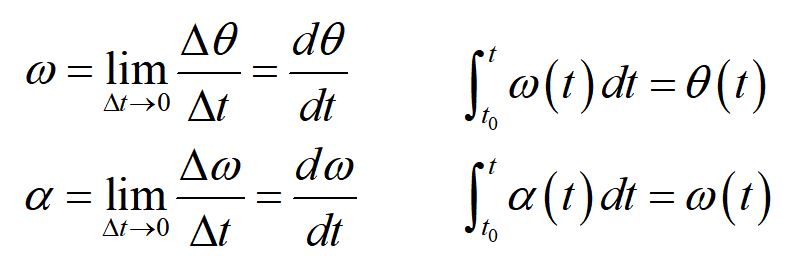

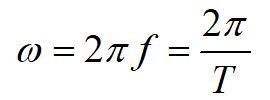

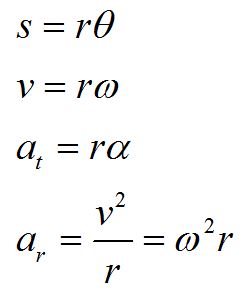
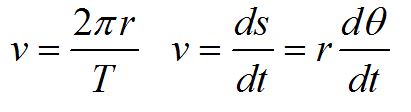
We can relate the angular variables to the translational variables using the arclength formula. Here, we have defined the tangential acceleration at and the radial acceleration ar. To completely define acceleration in three dimensions, we can include the acceleration in the z-direction az.
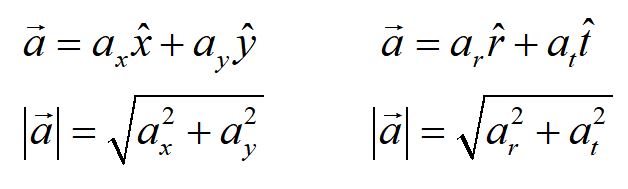
The acceleration vector for circular motion, in polar coordinates, is mathematically equivalent to the acceleration vector in Cartesian coordinates. In both cases, the components are independent, in that they are perpendicular to each other. Acceleration in polar coordinates is used for rotating systems as a convenience.
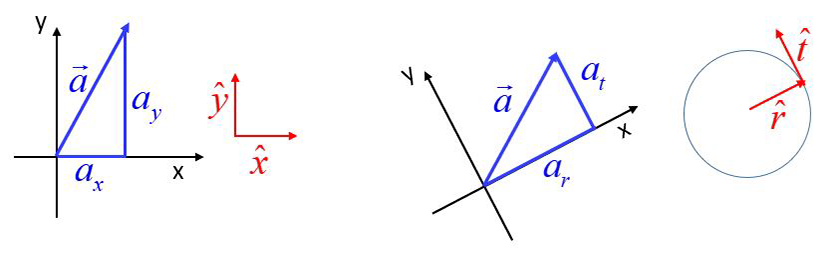
Here we show the same acceleration vector represented in rectangular coordinates and in polar coordinates. In rectangular coordinates the vector is resolved along the x and y-axes and can be defined using the associated unit vectors x-hat and y-hat. In polar coordinates, the same acceleration vector is resolved into coordinates in the rotated frame of the r-axis (radial axis) and t-axis (tangential axis) and can be defined using the associated unit vectors r-hat and t-hat.
It is important to note that these accelerations are two representations of translational acceleration, differing in coordinate system only. The acceleration of an object can be defined by either form. We choose the form that is most convenient for the motion of the object in question.
Angular acceleration, on the other hand, is a different kind of quantity. It defines the motion of rotation, not of translation.
Constant angular acceleration
For the case of constant angular acceleration, angular kinematics correlates directly to translational kinematics. Equations for position, velocity and acceleration are similar in form to equations for angle, angular velocity and angular acceleration.
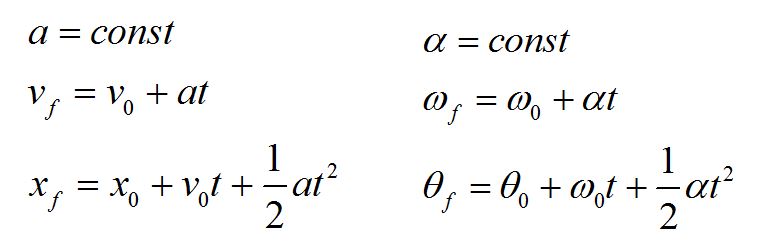
The left column gives the equations for linear kinematics in one dimension for the case of constant acceleration. The equations on the right are the corresponding angular kinematic equations for circular motion for constant angular acceleration.
Uniform circular motion
Uniform circular motion is the special case where the speed of the particle is constant. The velocity is not constant, as the direction is changing.
Let's review vectors a bit.
Practice problem
1. Which way does the vector v2 - v1 point?
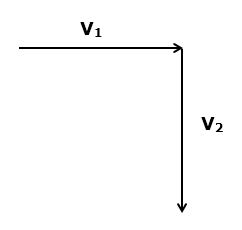
A. NE
B. SE
C. SW
D. NW
E. None of the above
Consider the diagram below. Which direction does v2 - v1 point? How about v3 - v2? How about v4 - v3?
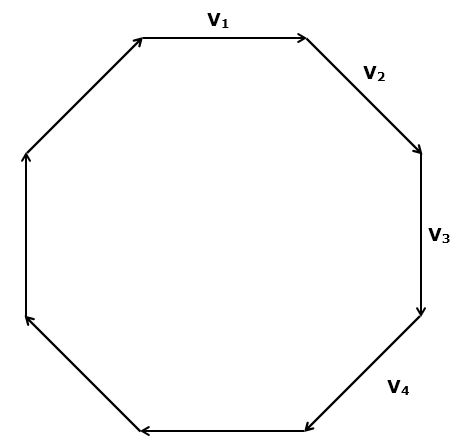
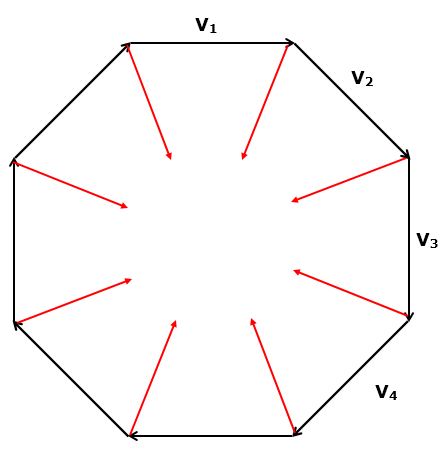

Derive radial acceleration

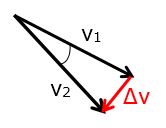
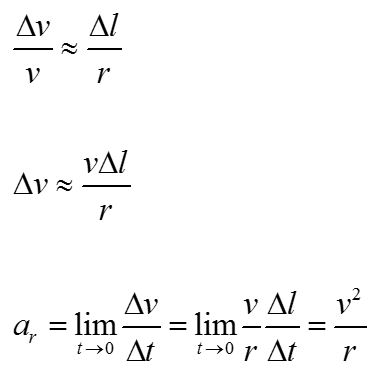
For uniform circular motion, the magnitudes of the velocity vectors are equal: v1 = v2. The velocity vectors are at right angles to the radial vectors, so the triangle made by the velocity vectors is similar (in the geometric sense) to the triangle made by the radial vectors.
These similar triangles provide a method for deriving a convenient form of the radial acceleration. For circular motion, the direction of the radial acceleration always points toward the center of the circle.
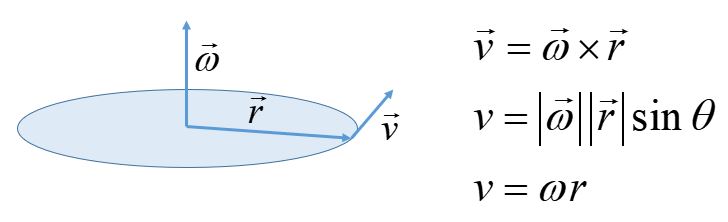
We find the direction of the angular velocity by using the more rigorous definition of velocity as the cross product of the angular velocity and the radial vector.
The particle moves in a circular path, defining a plane. The velocity is tangential to the circle, so it is perpendicular to the radial vector. The motion can be clockwise or counterclockwise. The angular velocity is a vector so it needs to have magnitude and direction. We would like to describe the three vectors in a common orthogonal basis.
We define the direction of omega as perpendicular to the plane and choose the direction (upward or downward) using the right-hand rule for cross products.
The direction of angular acceleration is related to the direction of angular velocity similarly to the way translational acceleration (in 1-D) is related to translational velocity.
The angular velocity defines the direction as out of the plane or into the plane. If the angular speed is increasing, the angular acceleration has the same direction. If the angular speed is decreasing, the angular acceleration has the opposite direction.

Image source