Sine waves
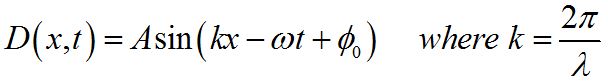
This equation describes a sine wave propagating in the positive x direction. During one period of time, the wave moves forward one wavelength.
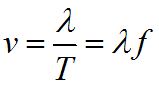
The speed of the wave is its distance traveled, divided by the time that has passed. This can also be written as the wavelength multiplied by the frequency. It is important to note that the frequency is that of the source of the wave. The speed of the wave depends on the medium. The wavelength that results depends on the source and the medium.
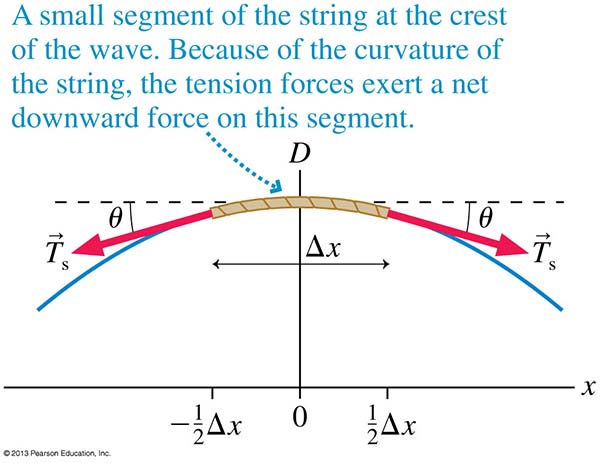

The speed of a wave traveling on a string can also be found in terms of the tension in the string and the linear density of the string. The larger the tension, the larger the restoring force on the string. This means that individual particles move toward equilibrium faster, so the wave propagates faster. The linear density is the mass term, carrying inertia. Higher density results in slower wave speed.

Phase difference
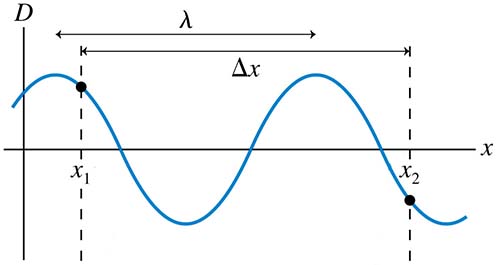
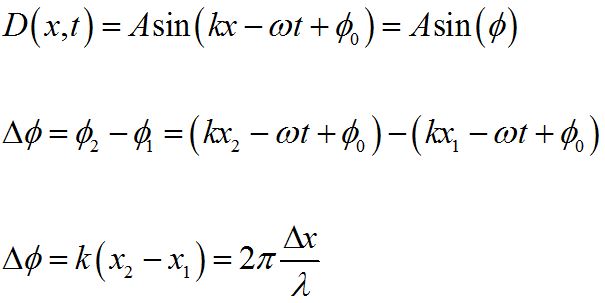

© 2013 Pearson Education, Inc
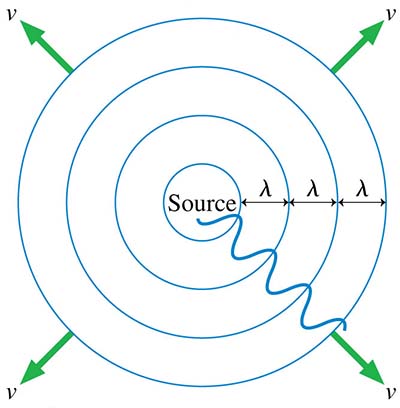
Waves can also propagate in two or three dimensions. As shown here, the wave crests mark the circular (or spherical) wave front that propagates radially outward at speed v. When the wave has propagated a considerable distance from the source, the curvature of the wave front becomes so small that the wave can be approximated as a plane wave.
© 2013 Pearson Education, Inc