1-D kinematics example problem

Two cars emerge from a tunnel at the same time (they are side by side). Car A is traveling at a constant speed of 30 m/s (about 67 mph). Car B is traveling at speed of 20 m/s (about 45 mph) and is accelerating at a constant rate of 3.0 m/s2. Car A initially pulls ahead of Car B, but eventually Car B catches up. How far have the cars traveled past the tunnel when they are again alongside each other? How fast are they each going?
Required solution format
1. Understand the problem and devise a plan
a. Translate the problem
Two cars start at the same position. Car A is faster than Car B but is moving at constant speed. Car B will fall behind, but is accelerating, so will catch up to Car A.
What is given and what will be determined? Translate the problem statement into math, using the form "symbol equals number units."
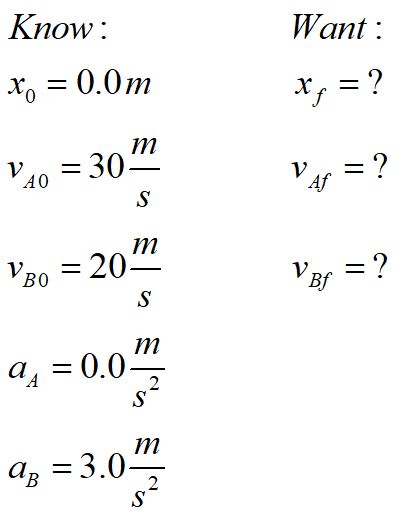
b. Determine applicable concepts and/or laws and assumptions and/or simplifications
Applicable concepts
- 1-D kinematics
Assumptions
What assumptions have we made?
- The cars can be treated as particles
- The cars are traveling parallel to each other
- The cars are traveling in a straight line
2. Represent the problem physically and mathematically
a. Represent physically: Draw an appropriate type of physical representation such as a diagram and/or graph
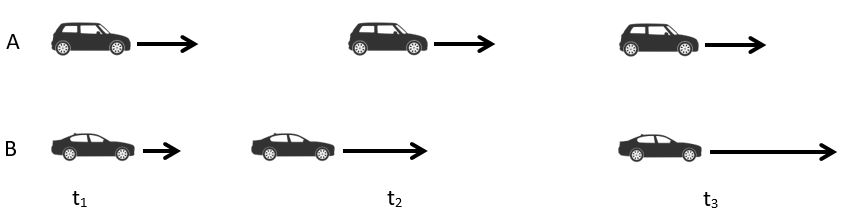
The diagram displays pictorially what happens in the problem.
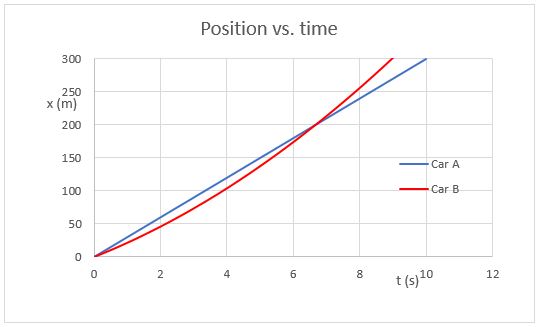
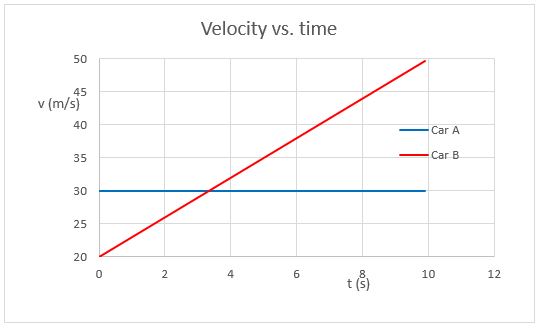
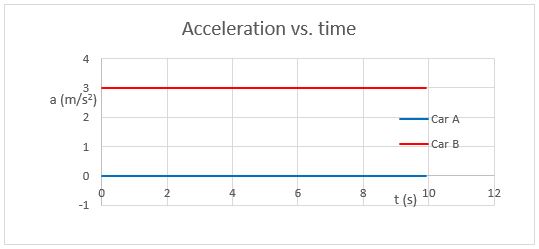
Note that there are two places where the lines cross. The intersection in the position vs. time graph indicates when the two cars are at the same place at the same time. The intersection in the velocity vs. time graph indicates when the two cars have the same speed.
In your homework, your graphs need to be conceptually correct. Note that the time when the cars have the same speed occurs before the time when they are at the same position. This makes sense, since the accelerating car will match the speed of the car with constant speed, and then move faster to catch up.
Also, the graphs should be internally consistent. Note that when the cars are at the same place, the slope of Car B is greater than that of Car A. This is consistent with the fact that Car B is shown to be going faster at that time.
b. Represent the concepts and/or laws mathematically
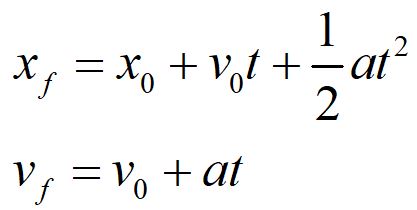
We begin by indicating the general equations appropriate for constant acceleration kinematic problems.
3. Solve for unknown quantities
Now we use the general equations we identified to solve our particular problem.
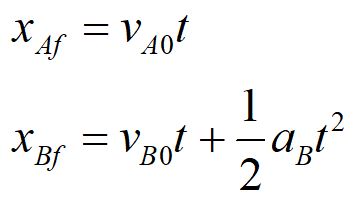
We modify the position equation for our problem. We have dropped the x0 terms, since we can set x0 = 0 at the tunnel exit. We have also dropped the acceleration for Car A, since it is zero.
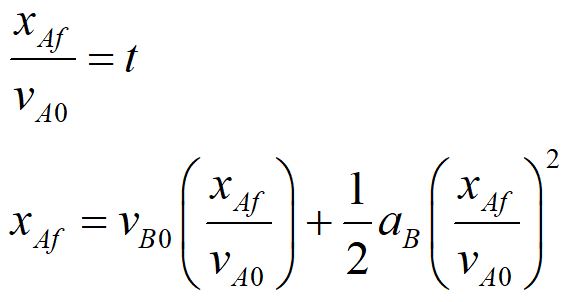
We choose a strategy of substitution. Since we are solving for the point where both cars are at the same position and time, we can solve the simpler Car A equation for t and substitute into the Car B equation. We can also substitute xAF for xBF.
Now we can algebraically solve for the variable we want. Now we will completely solve symbolically before inserting known values.
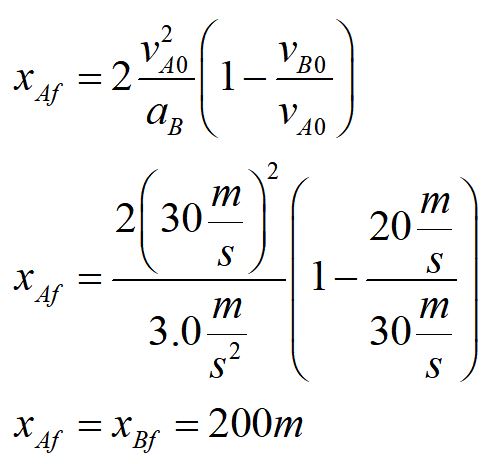
We have symbolically solved for the position. We check to make sure that our answer is completely in terms of given variables. We substitute in known values to get our final answer.
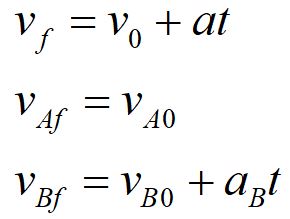
Now we need to find our velocities at that time. We can use the value we found for position to find the time in question. We begin by showing the general form of the velocity equation, and then the specific forms for Car A and Car B.
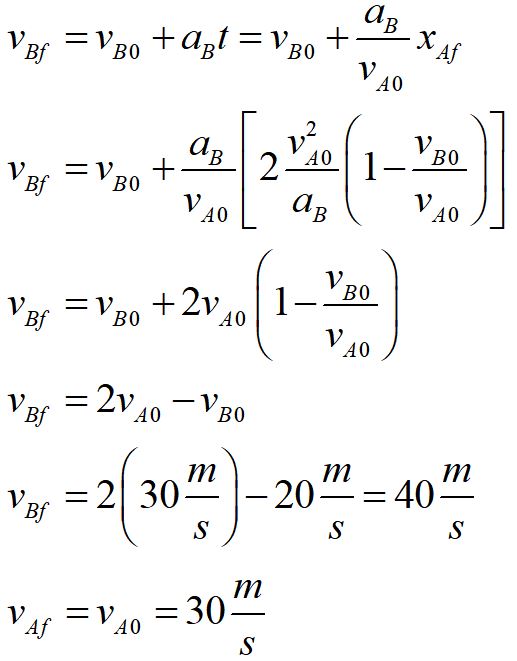
Now we substitute in our expression for time and simplify. Notice that we solved our equation completely in terms of given variables.
4. Is the answer reasonable? Does it make physical sense?
There are three parts to the checks for reasonableness: Units check, Order of magnitude, and limiting cases.
First, we will check the units.
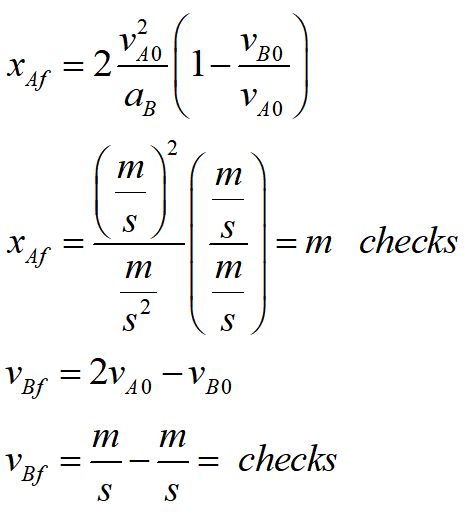
For each of our answers, we have explicitly checked to make sure the units are consistent.
For our order of magnitude check, we consider the values of our answers. Do they seem like reasonable numbers for the situation?
It is physically reasonable that our accelerating car could catch up and overtake Car A in 200 meters, given the known quantities of velocity and acceleration. Our final velocity for Car B is somewhat higher than that for Car A, so that makes sense. Our final velocity for Car B is pretty fast. 40 m/s is about 89 mph. This is possible...
Also, it is good to see that our answers are consistent with our position vs. time graph and our velocity vs. time graph.

For our limiting cases check, we will consider how increasing or decreasing the variables in our solutions affects the answers.
For the final position, there are three variables to consider, vA0, vB0 and aB. Larger vA0 indicates larger xAf, since the term in the numerator dominates. This makes physical sense, since the faster Car A is moving, the more time it will take Car B to catch up, so the farther they travel.
vB0 is in the numerator, but it is in a term being subtracted from 1, so larger vB0 indicates smaller distance traveled when the cars meet up. This makes sense, since the faster Car B is moving at the start, the quicker it will catch up to Car A.
aB is in the denominator, so mathematically larger aB indicates a smaller final distance. This makes sense, if Car B is speeding up at a greater rate, it will catch up in a shorter distance.
We also need to consider limiting cases for the final velocity of Car B (Car A's case is trivial). Here, we have two variables to consider, vA0 and vB0. Larger vA0 gives larger VBf, which makes sense since the faster Car A is moving, the faster Car B will be moving when it catches up. Also, larger vB0 infers larger vBf, which makes sense since Car B is undergoing constant positive acceleration.
