
Circular motion in a plane
- Fictitious forces
- Uniform circular motion
- Nonuniform circular motion
- Circular orbits
Newton's second law is a vector equation, so it can be broken into components.
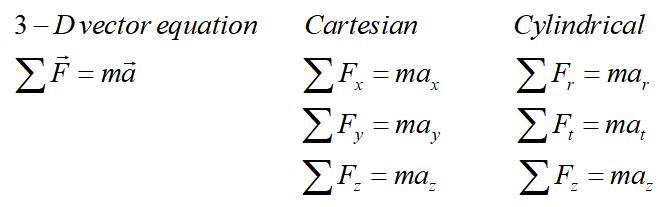
In this section, we will address motion in a plane, with particular focus on circular motion. In general, an object can be spiraling in a third dimension. In 2-D motion, the motion of the object is constrained to a plane, so we need only consider acceleration tangential to the circle and radial acceleration. Even in the case of uniform circular motion, where the speed of the object is constant, radial acceleration is not zero because the velocity vectors are changing direction.
Fictitious forces
Imagine riding in a fast-moving car that is turning a corner. You feel as though some force is pushing you outward, toward the car door until you feel yourself pushing against the door.
What you are experiencing is Newton's first law. You are a massive object that will move in a straight line at constant speed unless acted on by an unbalanced force. Your body wants to keep going straight and the car door constrains you to change direction.
Fictitious force: The force that seems to be pulling you toward the door is not a real force, it is what we call a "fictitious force." There is not an unseen force pulling you toward the door. You are just obeying Newton's first law.
Centrifugal force: The centrifugal force is a fictitious force that seems to pull you outward toward the car door.
Centripetal force: Centrifugal means "center-seeking." A centripetal force is one that involves centripetal acceleration in uniform circular motion. It is not a new force, it is just a way of designating this special case. In the turning car, the centripetal force is the normal force of the car door on you.
Uniform circular motion
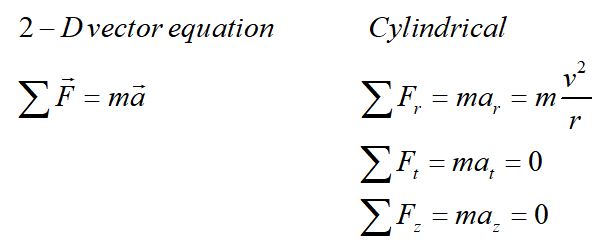
Uniform circular motion is motion in a circle with constant speed.
The direction of the velocity is changing but the magnitude of the velocity is not changing. We define the plane of motion in the r-t plane for the radial and tangential components.
Sample problem
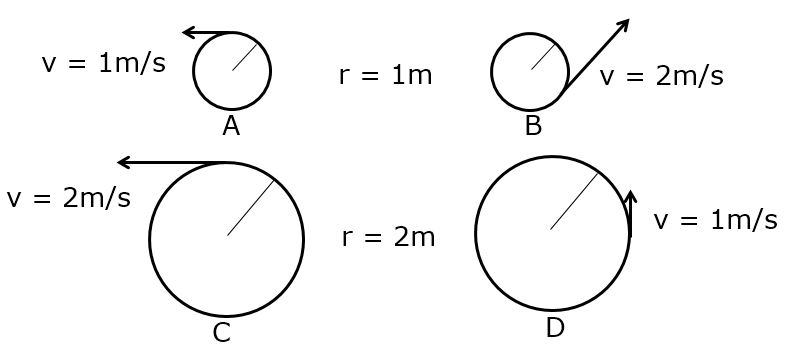
The diagrams below show velocity vectors of objects in uniform circular motion. Please rank their radial accelerations.
Non-uniform circular motion

For non-uniform circular motion, the speed is not constant. The object is constrained to move in a circle in a plane, but both the magnitude and the direction of the velocity are changing.
The radial equation for non-uniform circular motion has the same form as for uniform circular motion and is true for any instant in time, for the speed at that time. By definition, the radius is constant.
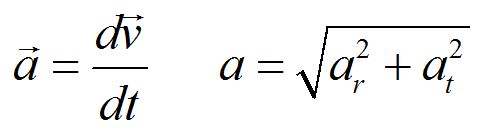
To find the magnitude of the total acceleration, the radial and tangential components must be added as vectors.
Image source