Projectile motion
By definition, a projectile is an object that has been launched and is in motion without any energy source propelling it, such as an engine.

For our study of projectile motion, we will disregard air resistance.
Projectile motion is inherently three dimensional motion, but we can always rotate our coordinate axis so that the motion lies in a plane containing two of the axes. This simplifies our mathematical construction so that we can solve a two dimensional problem.
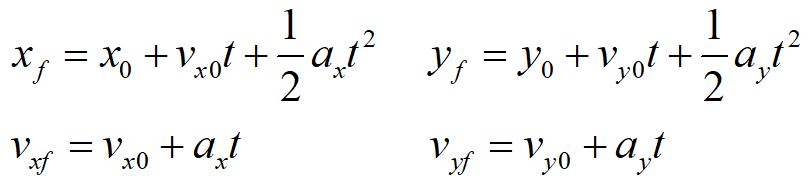
The general kinematics equations for constant acceleration are identical to those for one dimensional motion, only now we consider the vector equations in two directions.
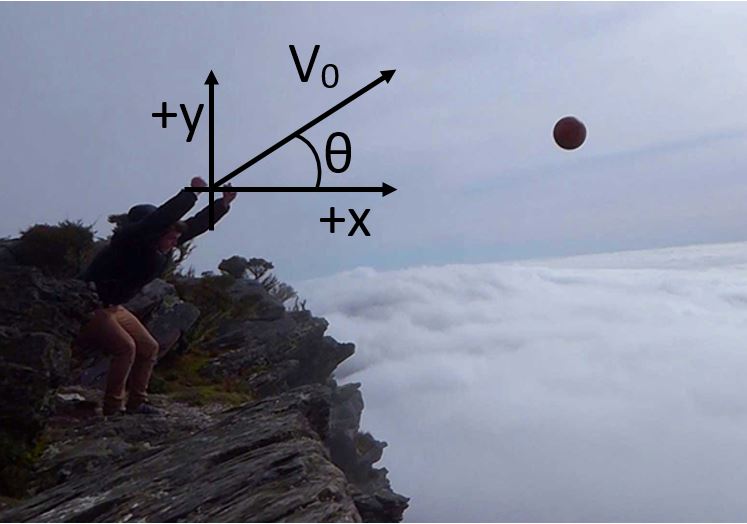
We want our choice of coordinate system to make the calculations as easy as possible. For projectile motion, it makes sense to choose one coordinate axis to be perpendicular to the ground. This means that the acceleration due to the gravitational force will be entirely in the direction of the vertical axis. We will choose this to be our +y axis.
We choose the +x axis parallel to the ground. Since we are not including air resistance, the acceleration in the x direction is zero.
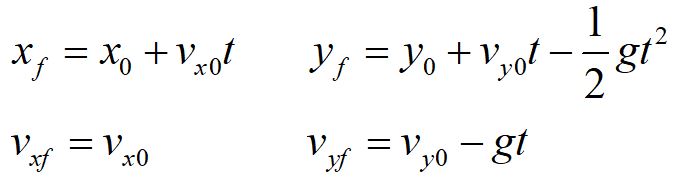
Our simplified equations for projectile motion include the fact that the acceleration due to gravity can be considered constant near the surface of Earth, and takes the value g. For our choice of coordinate axes, the acceleration due to gravity is in the negative y direction.
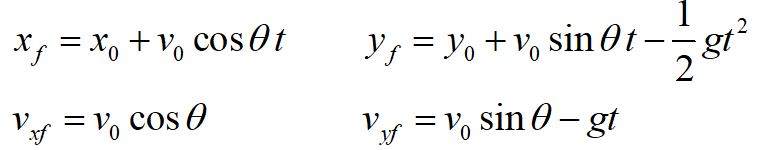

Sample problem

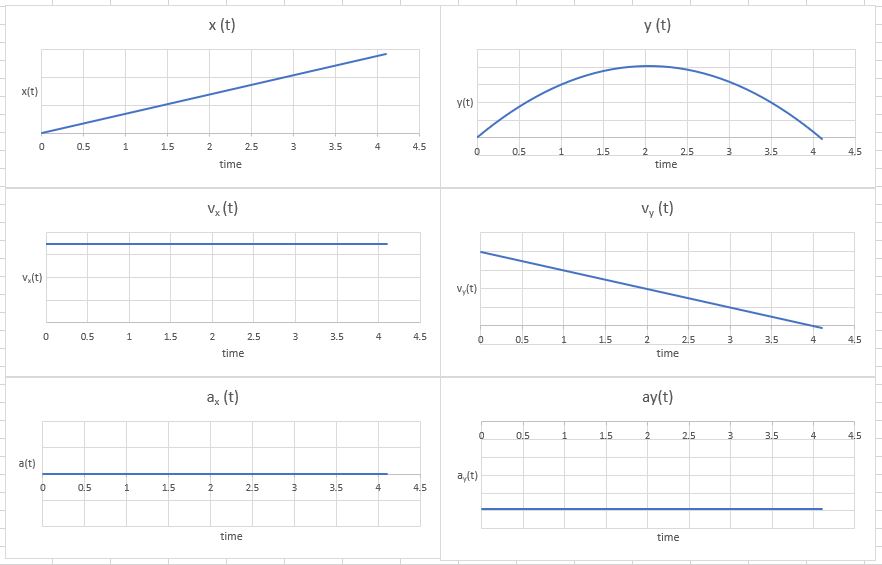
We make the general plots for 2-D kinematics and use them to plan our strategy.
We see that the y-velocity goes to zero at the top of the trajectory. We can use v(t) equation to solve for that time, and calculate yf at that time to see how high the particle will go.
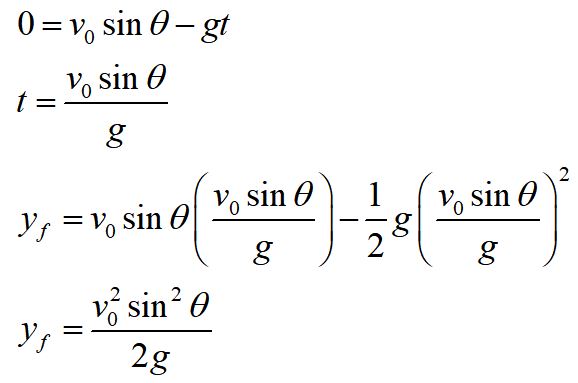
This gives us our maximum height for the projectile launched at a given angle.
Now we need to see how far the projectile goes in the x-direction.
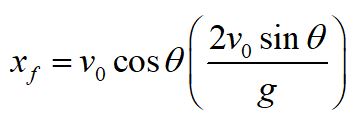
We can simplify this equation using a trig identity:
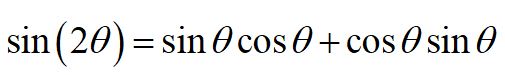
This gives us the form:
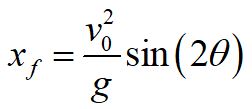
By symmetry, we can use twice that time to calculate how far the particle goes in the x-direction. We will take the initial x and y position as the origin.
Please note that this equation is only valid if the particle lands at the same height at which it was launched.
Our units check. Reality check: larger g would make smaller time in the air, smaller height and horizontal distance traveled.
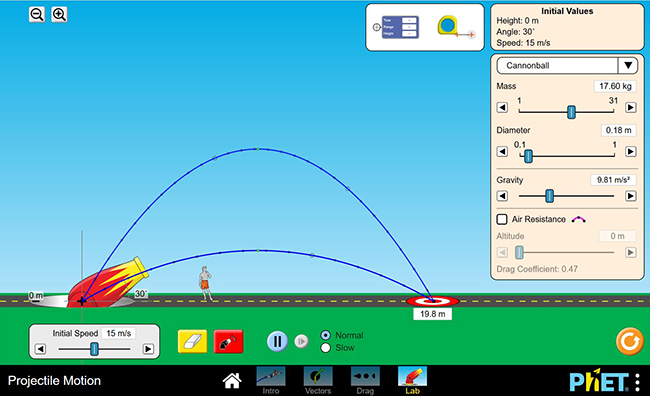
It is important to note that given an initial velocity and launch angle, only one range is possible. However, there are two different angles that can give the same range for the same initial velocity.

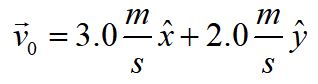
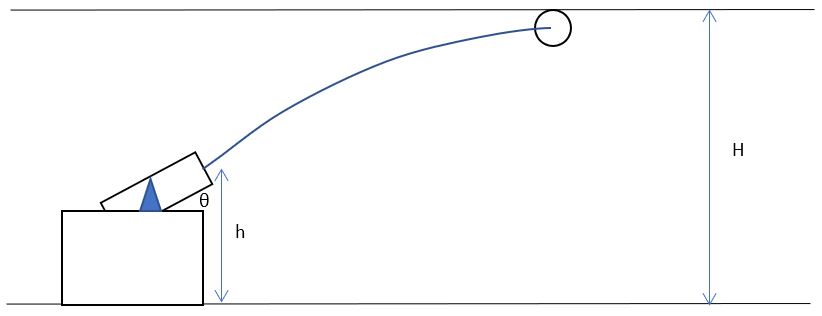
4. A marble gun shoots marbles of diameter d. When it is positioned such that the center of its barrel is a height h above the floor and its barrel is parallel to the floor, a marble fired from the gun hits the floor a distance D from the end of the barrel.
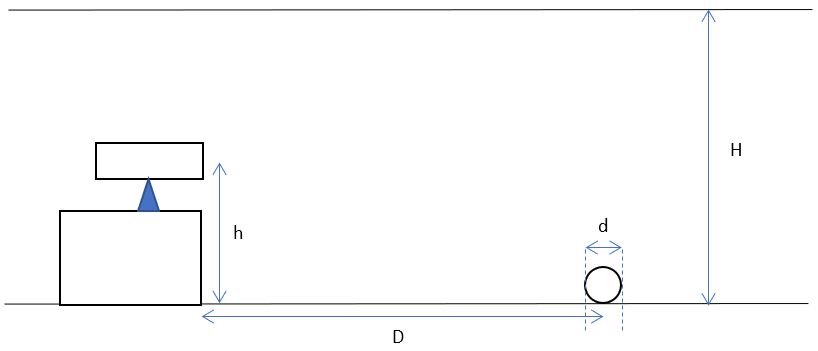
Now you rotate the gun such that the end of the barrel is still h above the floor, but now the barrel makes an angle θ with the parallel. What angle θ will allow you to just graze the ceiling at height H above the floor?