Introduction to PH 211
Physics is more than just a bunch of facts to be memorized or problems to be solved, it is a living discipline. Learning the basics of physics promotes seeing your everyday world in a whole new way. Physical models can be used to describe fundamental natures of systems, often by making simplifications. Once the simplified system is understood, more aspects of physics can be added to model an increasingly complicated system.

How fast will the skier be going at the bottom of the slope? To answer a question like this, we need to decide what approximations are appropriate. Do we need to take the shape of the person into account? Can we neglect friction? What about air resistance? Problem solving is a very important aspect of physics, and learning how to break down a physical situation is of utmost importance.
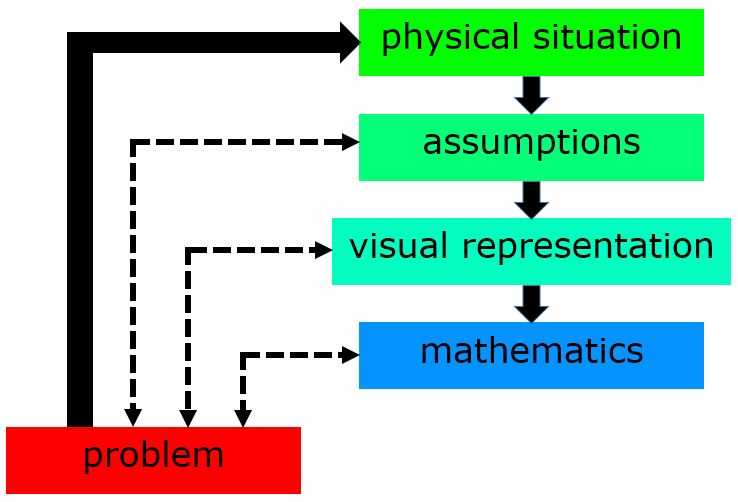
Problem solving begins with understanding the physical system involved and application of the appropriate underlying assumptions. Next, draw a good diagram. The diagram should then be used to create appropriate graphs or diagrams, such as free-body diagrams. The graph or diagram is used to construct a set of mathematical equations. One of the major flaws in the way folks typically approach physics problems is to jump right to the math, missing the underlying understanding of the system. As the systems become more difficult, paying attention to the underlying physics becomes increasingly important.
Learning a good approach to problem solving is the first step, but applying this approach to your everyday homework problems takes discipline. All too often, people understand how to approach problems in physics, but then when confronted with a tough problem, they tend to forget about the physical situation and go straight to hunting for an equation that looks appropriate.
One reason why this quick-fix approach fails is that many physics problems are multi-layered. There can be a problem nested within a problem that needs to be considered. One equation may not fit the situation. Always start by analyzing the physical situation, and go back to the situation while working through the problem.
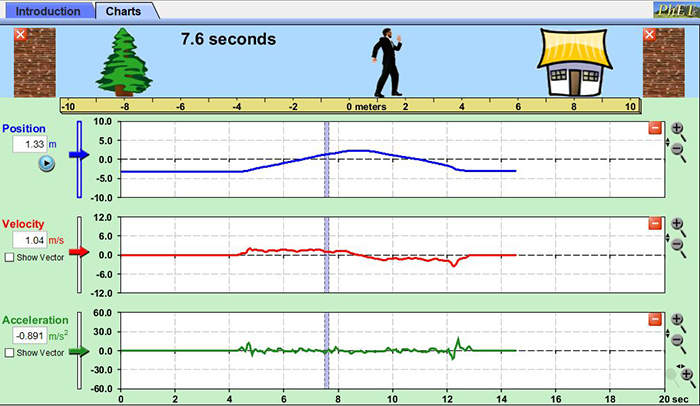
Incorporating an appropriate graphical approach is also very important in problem solving. The graphs provide information that can then be translated into a mathematical representation.
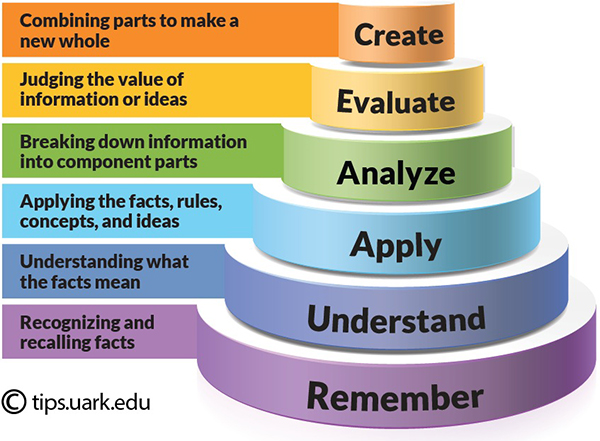
Bloom's taxonomy suggests that higher levels of learning require metacognition, or awareness of the thinking process. The lowest level of learning is just remembering what you have been told, and repeating it back. Higher levels of problem solving need more awareness. Being successful in the physics discipline strongly depends higher order learning, such as being able to combine concepts learned in simple problems in new situations.
Physics concepts take time to gel. Steady, daily practice is the best way to insure that your mind has time to create links between all of the integral parts needed to understand the whole problem. Cramming has been shown to be a very ineffective way to learn in general, and this is especially true in physics.
Physical representations: One of the learning objectives in physics is to be able to work in multiple representations
- oral
- written
- diagram
- graphical
- symbolic
- mathematic
It is understood that individuals may have a "learning style" that is favored. Maybe a person learns more easily by listening to words than reading them, for example. In the past, the tendency was to focus on the preferred learning style. Modern pedagogy has a stronger approach that stresses focusing on the learning styles that are more challenging, to become fluent in all representations.
Newtonian mechanics
Physics frameworks
In this term, we will consider several frameworks dealing with problem-solving in Newtonian mechanics. Understanding when to apply a particular framework to a problem is essential. Sometimes, problems can be solved using multiple approaches, though one approach may offer an easier solution than another. Sometimes, an approach may not be applicable, and may lead to an incorrect solution.
Kinematics
Kinematics is a description of how things move. The basis of this approach involves scalar and vector quantities that vary over time: position, distance and displacement; speed and velocity, and acceleration. Projectile motion is one application of kinematics.
Dynamics
Dynamics is a study of why objects move. It involves concepts including force, mass, energy and momentum.
Forces
A force approach also utilizes vectors, but in a very different way. A net nonzero force on a massive object will result in that object's acceleration. Newton's three force laws can be used to analyze systems when forces are known. This framework can be used in static situations as well as dynamic situations. Static and kinetic friction can be included if the situation warrants.
Conservation of energy
Energy is a scalar quantity, so this framework has a fundamental difference from the previous vector approaches. The initial energy of a system is equal to the final energy of a system, unless some of the energy is transformed into matter, or is created from matter. This is the fundamental idea behind Einstein's famous equation E = mc2. If energy was not created or destroyed, we can use a conservation of energy approach to solve a problem.
We also define nonconservative energy as energy that cannot be transformed into a useful form that can do work. Friction is a form of nonconservative energy, as the heat produced by friction diffuses into the objects or surroundings and cannot be recovered to do work. Mechanical energy is defined as energy that can be conserved in the form of kinetic or potential energy. A conservation of energy framework is useful for problems where a beginning state and an end state can be defined in terms of positions or motions of the objects in the system. The work-kinetic energy theorem can be used to solve problems where there is no change in potential energy.
Conservation of momentum
Conservation of momentum is another vector framework that can be used in solving problems in physics. Momentum is defined as the product of mass and velocity. Momentum is conserved when there is no net outside force acting on a system. One good application of this framework is problems that involve collisions between two or more objects. If there is no net outside force acting on the objects, the initial momentum is equal to the final momentum of the system. This is a good approach to use when a beginning state and an end state can be defined. If an increment of time is involved, a momentum-impulse approach may be used.
Physics 211 is the first course in a three quarter sequence offered by the Oregon State University Physics Department in online Ecampus format.


